import unittest

def squared_ints(x): # calculate square by taking the sum of x x's
    sum_of_xs = 0
    for i in range(x):
        sum_of_xs += x
    return sum_of_xs

class test_units(unittest.TestCase):

    def test_squared(self):
        self.assertTrue(squared_ints(4) == 16)                  # check 'normal' case
        self.assertTrue(squared_ints(1000000) == 1000000000000) # check extreme case
        self.assertRaises(TypeError, squared_ints, "A string")  # check it breaks

test_units().test_squared()

from hypothesis import given
from hypothesis.strategies import integers, text

class test_units(unittest.TestCase):
    @given(x=integers(min_value=-1000000, max_value=1000000))
    def test_squared_integers(self, x):
        self.assertEqual(squared_ints(x), x*x)

    @given(s=text())
    def test_squared_text(self, s):
        self.assertRaises(TypeError, squared_ints, s)

test_units().test_squared_integers()
test_units().test_squared_text()

>>> Falsifying example: test_squared_integers(self=<__main__.test_units
testMethod=runTest>, x=-1)

# use trapezium rule to approximate integral
def trapezium(f, xs):
    return sum((xs[1:] - xs[:-1]) * 0.5 * (f(xs[1:]) + f(xs[:-1])))

# test on something we know: y = x
def y(x):
    return x

xs = numpy.linspace(0, 0.5)

print('Integral using trapezium rule is: {}'.format(trapezium(y, xs)))
print('Analytic solution is: {}'.format(0.5 * xs[-1]**2))

>>> Integral using trapezium rule is: 0.125
>>> Analytic solution is: 0.125

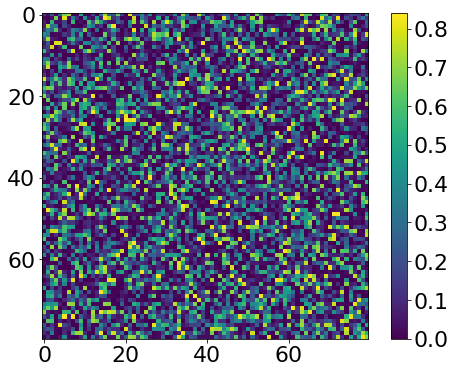
data = rand(80,80)                # declare some random data

def func(a):                       # function to apply to data
    return a**2 * numpy.sin(a)

# calculate & plot some function of random data
output = func(data)
plt.imshow(output);  plt.colorbar();   plt.show()

def test_limits(a):
    if numpy.all(a >= 0.) and numpy.all(a <= 0.842): return True
    return False

def test_average(a):
    if numpy.isclose(numpy.average(a), 0.223, rtol=5.e-2): return True
    return False

if test_limits(output):
	print('Function output within correct limits')
else:
	print('Function output is not within correct limits')
if test_average(output):
	print('Function output has correct average')
else:
	print('Function output does not have correct average')

>>> Function output within correct limits
>>> Function output has correct average

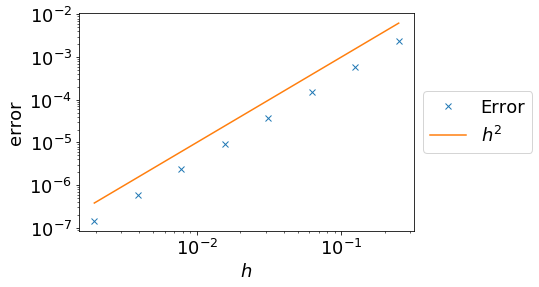
# use trapezium rule to find integral of sin x between 0,1
hs = numpy.array([1. / (4. * 2.**n) for n in range(8)])
errors = numpy.zeros_like(hs)

for i, h in enumerate(hs):
	xs = numpy.arange(0., 1.+h, h)
	ys = numpy.sin(xs)

	# use trapezium rule to approximate integral of sin(x)
	integral_approx = sum((xs[1:] - xs[:-1]) *
			  0.5 * (ys[1:] + ys[:-1]))
	errors[i] = -numpy.cos(1) + numpy.cos(0) - integral_approx

plt.loglog(hs, errors, 'x', label='Error')
plt.plot(hs, 0.1*hs**2, label=r'$h^2$')
plt.xlabel(r'$h$'); plt.ylabel('error')