In June of this year, I submitted the final corrections to my PhD thesis, Multiscale modelling of neutron star oceans. Now that I have put a few months between me and this date, I thought it would be nice to write a short outline of my thesis for those who might be interested but are too busy/have better things to do than read the full 200+ page pdf. This summary will contain no equations, a few pictures and hopefully not require a physics degree to understand.

Note: this is supposed to be a quick overview of my PhD work, so I won’t be including citations – for those I’m afraid you’ll have to check out my full thesis.

Neutron stars have oceans??

The motivation for my thesis was looking at Type I X-ray bursts. These are explosions which happen on the surfaces of neutron stars that which are in orbit around stars like our Sun. Neutron stars are extremely compact objects that form when massive stars die. They are about twice the mass of the Sun, but only 20km in diameter. Because they are so compact, neutron stars have very strong gravitational fields, so they pull (accrete) matter from the Sun-like stars. This makes its way to the surface of the stars, where over time it builds up to form a thin liquid ocean layer. This stealing of star matter continues until the ocean gets so hot and dense that it explodes. The explosion begins at a certain point on the surface (a hot spot), before very rapidly spreading throughout the entire ocean.

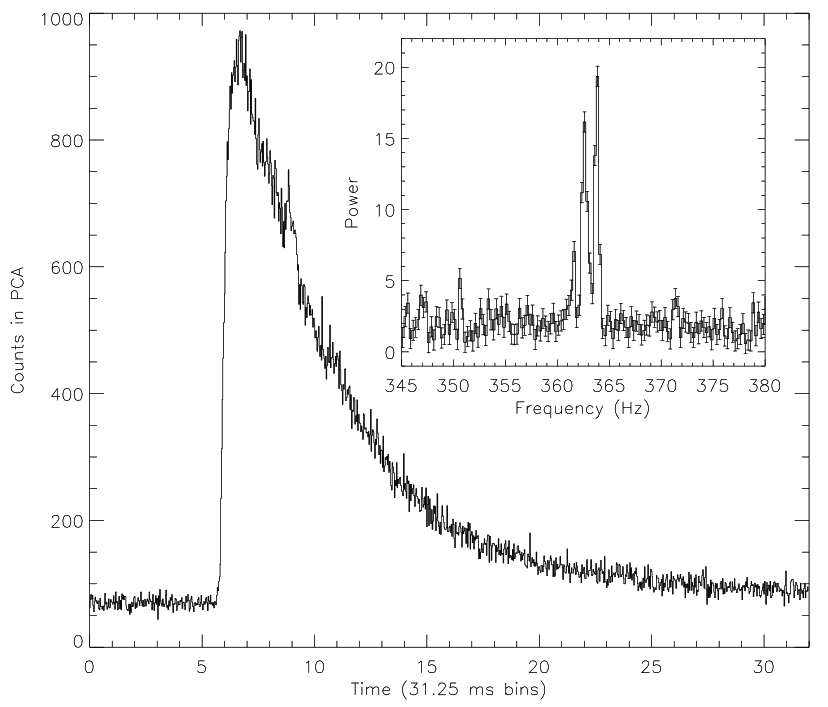
Observed X-ray radiation from an X-ray burst (Strohmayer+ 96).

We see this as a very sharp increase in the neutron star’s X-ray radiation. Unusually for an astrophysical process, we actually have lots of observations of these bursts as they reoccur every few hours. Unfortunately, this does not mean that we’re any closer to understanding the physics behind them. Neutron star oceans are very weird, extreme environments and there are lots of effects including rotation, magnetic fields and burning that play a part. One way to try and understand these bursts is with computer modelling. This is what I tried to do in my thesis.

Getting rid of sound with low Mach

When we do modelling of any kind of fluid flow, we’re typically limited by the speed of the fastest-moving thing in the simulation. If something is moving very quickly, we will need to do more steps in our simulation in order to properly capture its evolution. When the explosion spreads through the neutron star ocean, it does so at a speed that is much slower than the speed of sound. This means that if we use standard modelling techniques, we will be limited by this fast sound speed, despite the fact that we don’t really care what the sound waves are doing for this problem.

The low Mach number approximation is one way we can try and get around this problem. It is what is known as a soundproof model: by taking a certain limit of the normal fluid equations, we can effectively filter out sound waves. This means we can use much fewer steps in our simulation, and consequently can model a much longer period of time (or model a larger region or use higher resolution).

In my thesis, I took the Newtonian low Mach number approximation developed by Almgren+ 06 and extended it to general relativity. I implemented this relativistic version of the equations in the pyro code so I could compare it to the Newtonian version and check it behaved as expected in this limit.

Abstracting things with the Riemann problem

The Riemann problem is essentially a fancy name for what is actually a pretty simple setup: what happens if I have two states with different properties (e.g. density, temperature, velocity), initially separated by some solid barrier, then take the barrier away? The solutions of this problem for various types of fluid have been studied for decades, and consist of a series of waves such as shocks (supersonic waves) and rarefactions (subsonic waves). By simplifying complex systems to this much simpler problem, we can get estimates of the speeds of the waves that form in the complex system.

On the scale of the entire neutron star, the flame front becomes very thin: we can therefore think of it as a discontinuity and approximate it by the Riemann problem. We therefore looked at the reactive relativistic Riemann problem. We found that the relativistic version of this problem had some pretty cool effects that are not present in the standard Newtonian version: a very fast velocity moving parallel (tangential) to the discontinuity can change the nature of the solution (even in some cases turning a subsonic deflagration into a supersonic detonation), as can a change in the heat released during the reaction. Unfortunately, these effects only really become important for systems already on the verge of transitioning, so we highly doubt they’d be relevant for any real astrophysical systems.

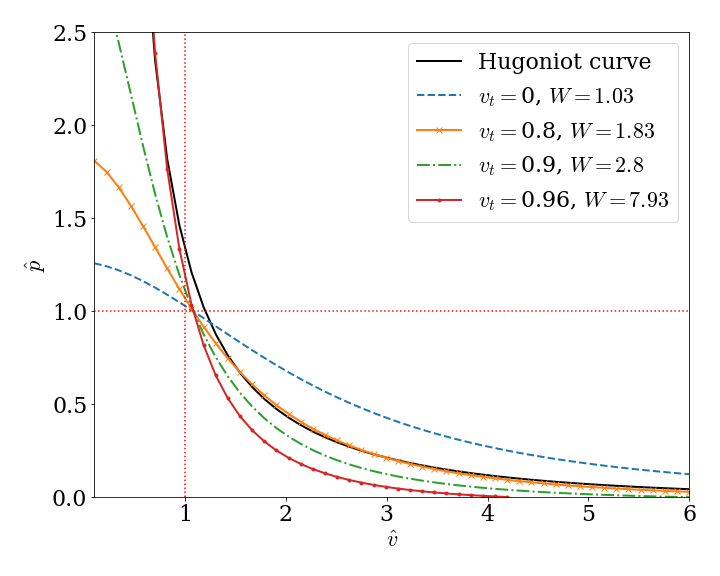
Varying the tangential velocity $v_t$ causes these curves (or *Rayleigh lines*) to move in a way that tells us the solutions of the Riemann problem change.

Hurricanes of fire in shallow water

The shallow water equations are yet another approximation of the standard fluid equations. They integrate the equations in the vertical direction, turning a 3d system into a 2d one. As the neutron star ocean is very shallow compared the size of the star (10m vs 10km), this is a good approximation to use if we care about the large scale behaviour of the flame. Neutron stars that produce X-ray bursts typically rotate a few hundred times per second, which means that on the surface the ocean experiences a very large Coriolis force. This is the same force that on the Earth produces hurricanes, and indeed it is thought that the Coriolis force whips the flame front into a hurricane of fire. As mentioned earlier, neutron stars have very strong gravitational fields. According to general relativity, rotating objects with very strong gravitational fields can produce some particularly weird physics known as frame dragging, where the spacetime outside the massive object get dragged along and deformed. I therefore wanted to see if this frame dragging could have effects on the fire hurricanes.

I did this by deriving a relativistic form of the shallow water equations and investigating their properties. I also built a simulation, swerve, that modelled the (reactive relativistic) multi-layer shallow water equations.

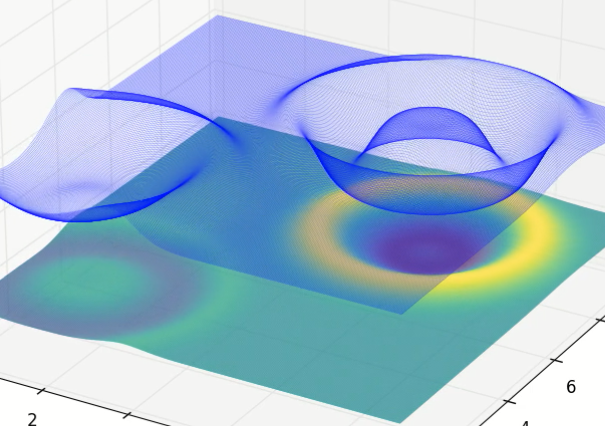
A multilayer shallow water simulation made using swerve.

Stitching things together with multiscale

The physics of X-ray bursts operates a very wide range of scales, from the large hurricane structures that are kilometres across, down to the turbulent burning reactions that operate on the scale of centimetres. This makes modelling them particularly challenging (on top of all the other issues I’ve mentioned above), as we need to model a very large area to capture the large scale physics but have fine enough resolution that we can also capture the important small scale physics. The method that I used here was multiscale modelling: essentially we use different physical models to model the physics at different scaless. The difficult part is trying to stitch these models together in a way that is consistent and makes sense.

If it’s so hard, why bother? Multiscale modelling has the potential to offer huge computational speed up over conventional models. Rather than using a model that is very accurate but very slow (computationally expensive) everywhere in the domain, we can use a simpler, faster model in regions of the domain where less interesting things are happening (e.g. away from the flame), and only use the more accurate model where we really need it (e.g. at the flame). It also makes sense for systems where very different physical processes operate at different scales. A model that is good at describing one physical process (e.g. burning) may be rubbish at describing another one (e.g. hurricanes).

The multiscale model I developed was made up of the shallow water model on the large scale and the standard compressible fluid equations on small scales. Stitching these models together has a number of challenges, the main one being that the shallow water equations are 2d and the fluid equations are 3d. When we first derive the shallow water equations, we essentially throw out all information about the system in the vertical direction (and also information to do with the thermodynamic energy). How do we reconstruct this information in order to match the shallow water model back up with the compressible one? The answer is that we have to make certain assumptions about the fluid at the boundary (e.g. I assumed it was in hydrostatic equilibrium and adiabatic).

I implemented this model by hacking it into a couple of existing codes - Castro and AMReX. This first attempt at a multiscale model showed promise – features were able to pass across the boundary between the models – however, it quickly became unstable if any large features tried to pass through the interface. This suggests that the model matching is not yet quite correct and more sophisticated methods or better assumptions are needed.

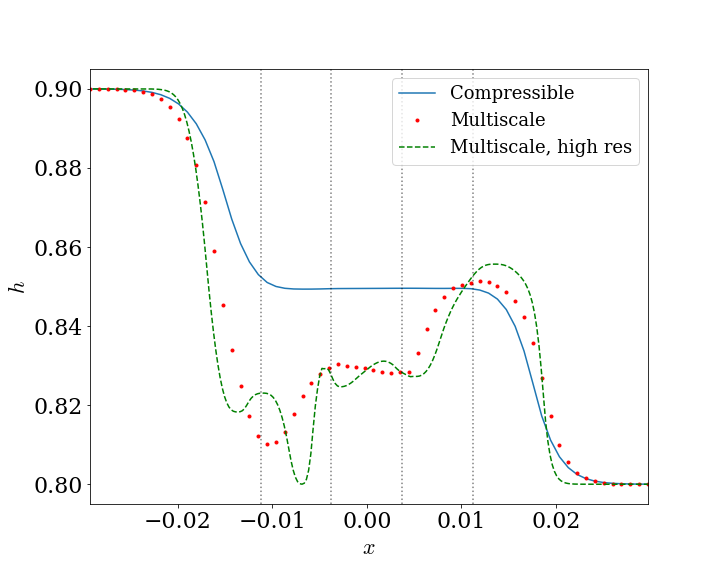
Test using the multiscale model compared against the compressible solution. The multiscale model is clearly a bit unstable in the middle region, but it does ok in the outer regions.

tl;dr of the tl;dr

Explosions happen on some neutron stars which we observe as bursts of X-rays. Modelling these explosions is hard as the physics is very extreme and complex. I looked at a load of different models at different scales, and stitched a couple of these models together to produce a multiscale model.